Applications of Matrix Multiplication, Dot Product, and Weighted Sum in Deep Learning

In deep learning, matrix multiplication, dot product, and weighted sum are core mathematical operations. These operations frequently appear in neural network forward propagation, weight updates, and attention mechanisms. Here's a detailed summary of these concepts.

Problem Description

What is matrix multiplication?

Problem Analysis

If matrix A has shape m×n and matrix B has shape n×p, then their product matrix C=A⋅B has shape m×p. We can see that n is eliminated, what happened there? Let's look at an example:

A=
[
  1 2
  3 4
]
B=
[
  5 6
  7 8
]

C =
[
  1 2 * 5 7, 1 2 * 6 8
  3 4 * 5 7, 3 4 * 6 8
]

=
[
  1*5+2*7,1*6+2*8
  3*5+4*7,3*6+4*8
]

In the final result, we see the appearance of dot product, which is actually the most basic calculation method in matrix multiplication.

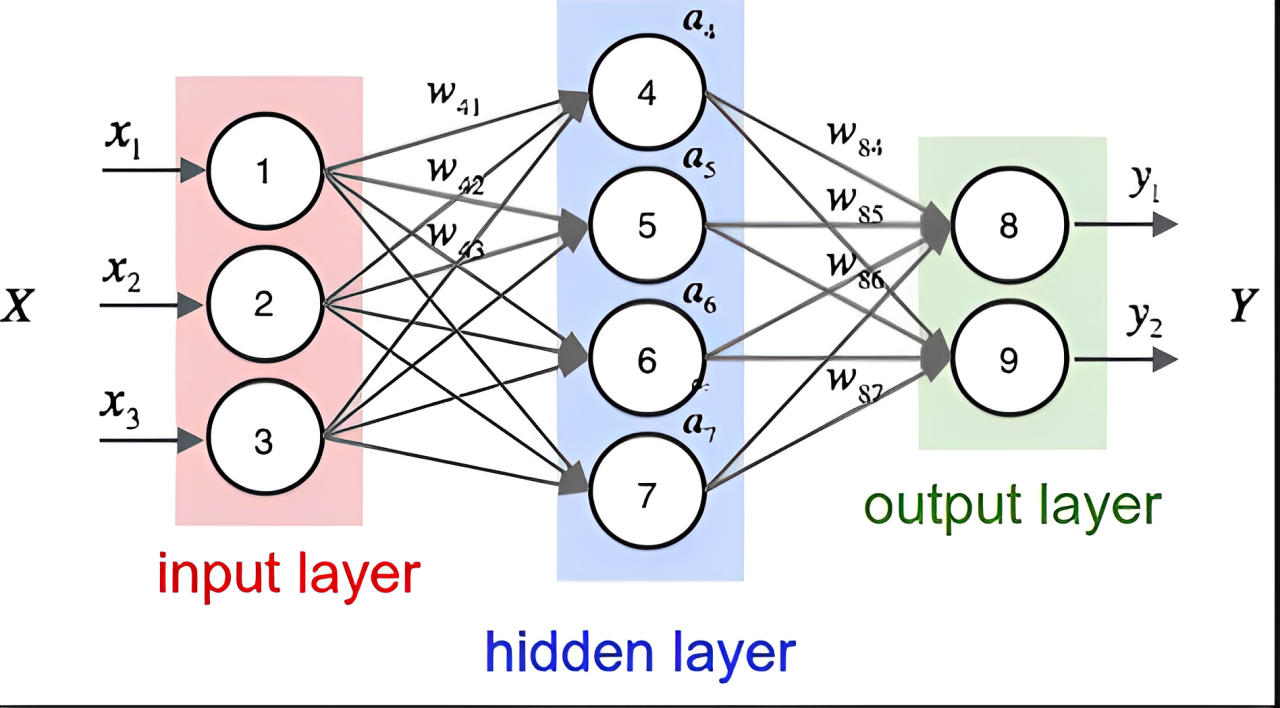
How is Matrix Multiplication Reflected in Neural Networks?

The output of a neuron can be represented as:

output=input⋅weights+bias

where input is the input matrix, weights is the weight matrix, and bias is the bias vector.

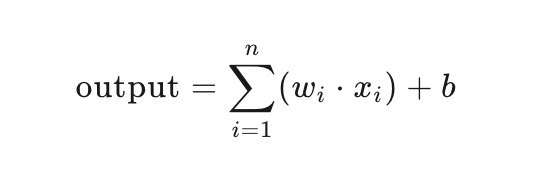
where wi is the weight, xi is the input, b is the bias, which is the dot product of the weight matrix and input matrix.

So we can see that a neuron is the result of a dot product in the matrix, just with an added bias term.

Three-Dimensional Matrices

Let's first understand three-dimensional matrices as batch matrix multiplication, where we need to fix the third dimension for calculation.

Problem Description

What does it mean to calculate with a fixed third dimension?

Problem Analysis

Assume:

• Matrix A has shape (n,m,p)
• Matrix B has shape (n,p,q)
• Result C has shape (n,m,q)

Do we see the pattern? It's actually just two-dimensional matrix calculation, In deep learning, this n is equivalent to the batch size, the number of samples, having a third dimension allows us to perform batch calculations on samples.

Calculation Method in CNN 3D Matrices

Let's cover the basic concept: In Convolutional Neural Networks (CNN), the multiplication of a local region of the input image with the convolution kernel (filter) indeed results in a scalar (single value), achieved through dot product (inner product) operation.

Let's use numbers directly:

The input is 2x2x3 (3-channel RGB image), the convolution kernel is 2x2x3 also with 3 channels, multiplying the input and convolution kernel will result in a 2x2x3 matrix.

The CNN concept is to perform convolution processing between the input image and convolution kernel, meaning we need to calculate the dot product of the matrices. We know how to calculate the dot product within a matrix, but for dot product between matrices, we actually flatten our matrices into one-dimensional matrices, multiply and sum them. So we can get the dot product results for three channels, and when we add these three channels together, we get one feature.

Attention Mechanism

Problem Description

In the transformer's attention mechanism scoring formula, there's also a dot product processing Q*K, why doesn't it result in a scalar?

Problem Analysis

It's actually Q multiplied by the transpose of K, not a dot product result, but a matrix multiplication calculation.