深度学习中的矩阵运算总结
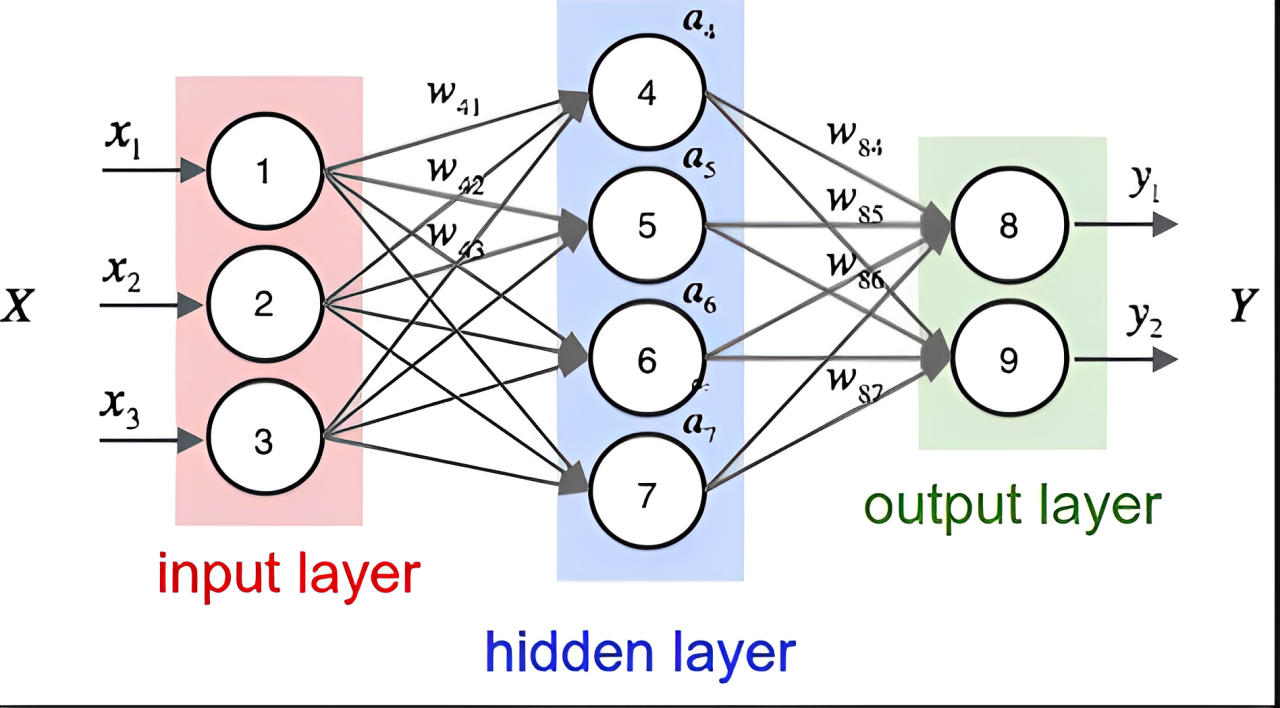
矩阵相乘、点积和加权求和在深度学习中的应用
2025-4-1
矩阵的相乘、点积和加权求和在深度学习中的应用
在深度学习中,矩阵相乘、点积和加权求和是核心的数学运算。这些运算在神经网络的前向传播、权重更新以及注意力机制等过程中频繁出现。以下是对这些概念的详细总结。
问题描述
什么是矩阵相乘?
问题分析
如果矩阵 A 的形状是 m×n,矩阵 B 的形状是 n×p,那么它们的乘积矩阵 C=A⋅B 的形状是 m×p。 我们可以看到 n 被约掉了,其中发生了什么?下面看一个例子:
A=
[
1 2
3 4
]
B=
[
5 6
7 8
]
C =
[
1 2 * 5 7, 1 2 * 6 8
3 4 * 5 7, 3 4 * 6 8
]
=
[
1*5+2*7,1*6+2*8
3*5+4*7,3*6+4*8
]
最后的结果我们看到了 点积 的出现对行吧,其实它是矩阵相乘中最基础的计算方式。
那么神经网络怎么体现矩阵相乘呢?
一个神经元的输出可以表示为:
output=input⋅weights+bias
其中,input 是输入矩阵,weights 是权重矩阵,bias 是偏置向量。
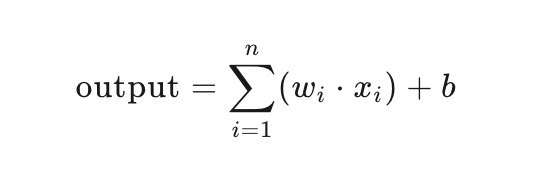
其中,wi,是权重,xi是输入,b 是偏置, 就是权重矩阵和输入矩阵的点积。
所以我们看到一个 神经元 就是矩阵中一个点积的结果,只是我们还多加了个偏置量。
三维矩阵
三维矩阵我们先理解为批量矩阵相乘,我们要固定第三维度来计算
问题描述
什么叫做固定第三个维度进行计算呢?
问题分析
假设:
- 矩阵A形状是(n,m,p)
- 矩阵B形状是(n,p,q)
- 结果C形状是(n,m,q)
我们看到了规律没有,其实也就是二维矩阵的计算, 那么我们在深度学习的时候,这个n 相当于就是 batch size 所谓的样本数量,有第三维度我们可以对样本进行批量计算
CNN三维矩阵中的计算方式
说下基本概念:在卷积神经网络(CNN)中,输入图像的局部区域与卷积核(filter)相乘后得到的确实是一个标量(单个数值),这是通过点积(内积)运算实现的
直接上数字:
输入是 2x2x3 (3通道的RGB图像),卷积核是 2x2x3 也是3通道,输入和卷积核相乘会得到一个 2x2x3 的矩阵,
CNN的概念是让输入图片和卷积核做卷积处理,也就是我们要求矩阵的 点积 结果,矩阵内的点积我们是知道的,但是矩阵跟矩阵的点积,其实就是把我们的矩阵展开乘一维矩阵再相乘,相加得到的结果,所以我们可以得到三个通道的点积结果,我们再把三个通道加起来就得到了一个特征
注意力机制
问题描述
transformer中的注意力机制得分的公式,也有个点积处理Q*K,为什么不是得到一个标量呢?
问题分析
其实是Q 乘以 K 的转置,不是点积的结果,是矩阵相乘的计算